This is the second article in my Quantum Mechanics series, following “Quantum Mechanics – Taking A Look At Quantum Entanglement”. After doing a little bit more research, I have discovered the Heisenberg Uncertainty Principle, which is kind of like a base for measurement in this scientific world. This post will help you to understand further concepts I plan on sharing in my future articles.
~~~~~
It’s not ‘there are some things you will never be sure of’, it’s ‘you can never be sure everything’. Those two are completely separate things.
Quantum mechanics is the vast study of particles, subatomic particles, etc. that entails many things. To some, quantum mechanics is extremely confusing, however, if you work with it step by step, you will get to learn many fascinating things. To begin to understand quantum mechanics, you have to start small, with measuring position & momentum and most importantly, figuring out the Heisenberg Uncertainty Principle, a statement that defines the nature of particles and subatomic particles making it an important subtopic in quantum mechanics. So what exactly is the Heisenberg Uncertainty Principle? In 1927, german physicist, Werner Heisenberg established that you can never simultaneously know the exact position and momentum of an object. How does this work? Well, in order to make sense of this complex theory, we have to go back to what quantum mechanics is described as – particles and waves. A particle has a position, so we know where it is in space. Waves are more like little disturbances like ripples in a pond. They can be in many places at once, so they don’t have an exact position. On the contrary, waves directly relate to momentum. A fast moving object has a lot of momentum and so do big heavy objects. Things with a lot of momentum have very short waves while things with little momentum have very long waves. A particle doesn’t have momentum. So, how can we have a quantum object with both position and momentum. You’re about to find out.
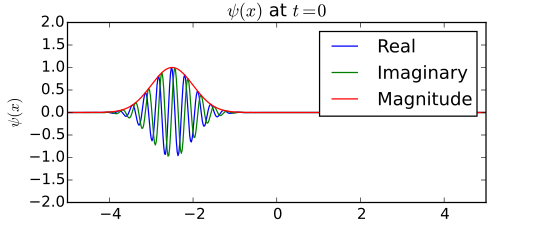
In order to create a quantum object with both position and momentum, we need to create a wave packet. This can be done by layering waves on top of waves, which would lead to small waves separated by distances of nothing at all. . With this method, we have narrowed down the position to the wave packet, however, we do not know what the exact position is inside the wave packet. As for the waves, since we layered many waves on top of each other, the packet has a possibilility of different momenta. (See diagram) To be more certain about the position, you can layer more waves, but then you lose more certainty of the momentum. To find the momentum, you can take away layers of waves, but then you will be even more uncertain about the position. That is what the Heisenberg uncertainty principle is. In order to have something with both position and momentum, we need to lose certainty of both of them. The formula for Heisenberg’s uncertainty principle is (1) Δq x Δv > ħ/m. It is crucial to understand the Heisenberg Uncertainty Principle when studying quantum mechanics because it clarifies how to measure them and is the basis for what quantum mechanics revolves around.
The Heisenberg uncertainty principle certainly is quite an interesting theory. To add on, we can also use it to our advantage. Recent studies show that the heisenberg uncertainty principle allows us to send uncrackable messages through photons (light particles). Anyone who tries to intercept the message will be discovered due to the disturbance they make to the waves. For some food to chew on, here’s an example from an article by university professor Howard Wiseman – “You may have heard the anecdote about a woman who is stopped by a policeman who says: “I just measured your speed as 53.9 km/hr when you were in a 40 km/hr school zone.” She retorts: “Are you familiar with the Heisenberg Uncertainty Principle? If you are so sure about my speed, you can’t possibly know where my car was.””Do you think this would work? Thankfully not. This scenario would not count since the police officer would have been off on his position and momentum by only a tiny, insignificant amount meaning that the bus driver was still driving at about 50.93km/h in a 30km/h school zone. This principle applies only to particles and subatomic particles since they are so small, a ‘small distance’ would actually be quite a large one. But is important to remember when studying this uncertainty principle, as Heisenberg and many other physicists believe – a particle does not have a position or momentum, until you measure it.


